It is a surprise to many people today that there is even such a thing even exists - a field of mathematics that can be incorporated by visual artists into creating beautiful works of art. In fact, this did exist and in the West, architectural design, for example, incorporated its principles from the time of ancient Greeks up to the Second World War. As readers will be aware, I have been posting articles demonstrating how different buildings look as a result of this. it is effectively the study of the mathematics of pattern.
The starting point for the study is a beautiful object and consensus that it is beautiful - the cosmos or musical harmony for example. Then there is a psychological study by which the 'scientist' analyses the underlying mathematical order that people seem to be responding to.
The real test of the truth of whatever theories arise from this study is not so the coherence of the theory proposed - human reason is weak and liable to make errors (as any authentic natural scientist who still holds to the established scientific method will attest). No matter how elegant the theoretical justification appears to be, how sound the axioms, or how watertight the logic, we cannot be sure that this alone is a measure of its truth. No, the test is that when it is applied in some new way, it works repeatedly. So in the field of the mathematics of beauty, when artifacts are created that incorporate the mathematical principles, people find it beautiful.
Beauty is a property that is difficult to test, given that there are many other factors contributing to the beauty of an object, and that we cannot be sure whose powers to judge what is beautiful are well formed. The best test that we have therefore, is not the opinion of the few, but rather general opinion over generations. What we might call 'common taste', drawing an analogy with common sense. The usual term for this common taste is tradition. This is why if want to create a beautiful culture we look to tradition to guide us in the present. The strongest argument for the truth of the theories of the mathematics of beauty is the fact that generations of people have marvelled at its beauty. The test of time increases the chances that we are not simply following the vagaries of contemporary fashion, which is not such a reliable guide.
If we want to train someone to be able to contribute to the culture beautifully, in any regard (not just art) then that training ought to include, I suggest, the study of the theory of the mathematics of beauty, and the study (including guided imitation) of a canon of traditional forms for which there is a general consensus that they are beautiful.
For any creative process, therefore, tradition is the rudder of the past that steers the barque of his present activity of creativity, while God is force that motions it forward through inspirational ideas of what it will be in the future, once created.
Resistance to the idea that mathematics can have anything with creativity runs deep today. The Romantic mindset runs deep even in conservatively minded artists and architects who wish to reesatablish the forms of the past. In my experience of discussing such matters with many of them, even these architects who have studied and are looking to reacreated classical forms as part of the training, will resist the idea that there is anything mathematical that they need to learn. Even artists who are studying the academic method of classical naturalism will assume that their intuition is enough.
The answer is that intution has a part to play, but a musical composer needs the theory before he can create a new and beautiful piece of music. Even Mozart and Beethoven, prodigies that they were, had music lessons and were taught some theory by their fathers.
Pontifex University's Mathematics of Beauty course, which is part of the Master of Sacred Arts program as a whole requires a study of the theory by looking at the work of figures such as Pythagoras, Plato, Aristotle, Boethius, Augustine Bonaventure, Aquinas, and recent summaries of the theories such as those by Rudolph Wittkower and Benedict XVI. This includes both the study of traditional harmony and proportion, and a philosophical examination of the nature of number itself, focussing on it's capacity to communicate both magnitude and symbolic meaning. There is conventional written examination of their understanding of these principles.
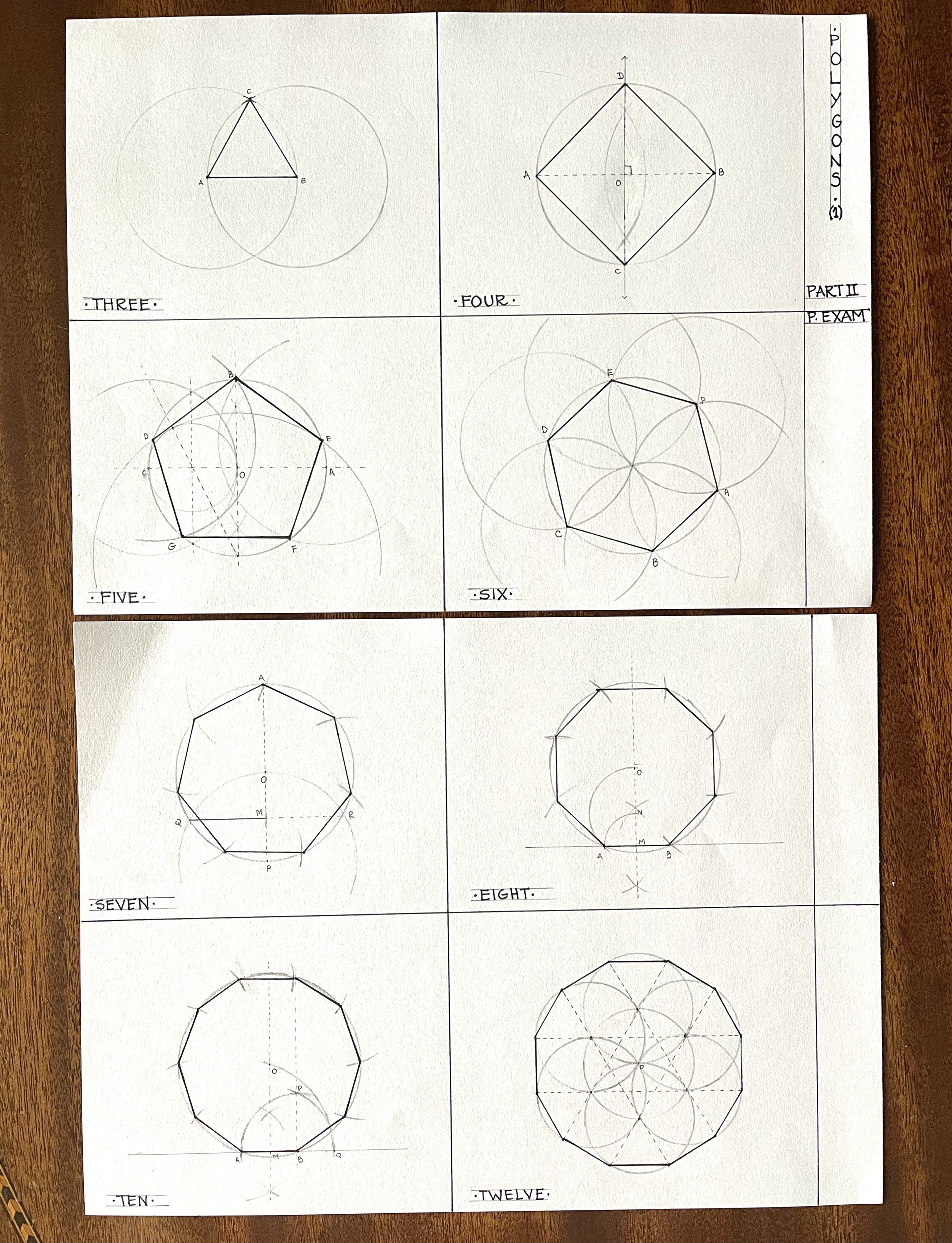
The practical element of this course requires the student to submit a portfolio of work that incorporates the mathematics into traditional geometric construction and patterns. Beginning with very basic principles of creating the primary geometric shapes from first principles - with only a pair of compasses and a straight edge - the student then has to create an Islamic-style patterned tile as might have been used in the Cathedral at Monreale in Sicily, for example. Then I ask the student to create a complex piece of opus sectile work based upon opus sectile and cosmati patterns of the Romanesque and early gothic periods respectively, such as might be found in the churches of Rome of the period.
The following are some submissions from student Daniela Diz who gave me permission to feature her excellent work here. First the musical scales of the discipline, basic geometric construction:
Then the geometric construction described by Plato called 'quadrature'. The student constructs a square and then creates another with, first, half the area, and second, twice the area.
There is a practical application to this historically. The ratio of the lenth of the side of the smaller square to the larger is 1:√2, while the ratio of the areas is 1:2. This is seen as a way of creating the geometric mean between between the two extremes of 1 and 2, represented as 1:√2::√2:2. If the smaller square is placed inside the larger so that the sides are parallel, then this becomes an example of a template for the dimensions of a cloistered walkway into a church by which, symbolically, we walk along the path of virtue, the temperate mean between the extremes of excess and deficiency.
Next we have a design based upon an Islamic tiled pattern. Islamic patterned art developed originally from that of Byzantine artists in conquered lands from the 7th century onwards and became quickly an art form in its own right. Over centuries, those Islamic patterns then became the basis for those used by Christians. Examples are common in Spain and perhaps some of the most famous examples are in the Norman churches of Sicily such as in Monreale.
Inlaid marble work from Monreale Cathedral, Sicily, 12th century AD
Finally here is an example of a chain of circles known as a 'guilloche'. The etymology of the word is incertain. The students was asked to choose between this and similar design based on circles called a quincunx and then choose how to decorate it based upon existing tile patterns.